
Опубликовано: Журнал общей биологии. 2005. Т. 66. № 4. С. 326–335. PDF
ЗНАЧЕНИЕ ПРАВИЛА ВИЛЛИСА ДЛЯ ТАКСОНОМИИ
© 2005 г. А.А. Поздняков
В таксономии соотношение частот родов и видов описывается ранговым распределением. Оно считается характерным для систематики и получило название правила, или закона Виллиса. Однако аналогичные распределения известны не только в других областях биологии, но и в научных дисциплинах, далеких от биологии. В биологии вне области систематики ранговые распределения известны в экологии (Голиков, 1976), морфологии (Корона, 1987), молекулярной биологии (Apic et al., 2001; Kuznetsov, 2003). Общим для указанных случаев является то, что эти распределения получены при ранжировании некоторых аспектов многообразия и касаются соотношения объемов получающихся классов. Очевидно, что в отдельных научных дисциплинах может быть дано свое объяснение полученным закономерностям, хотя нельзя исключать существования объяснения, пригодного для всех случаев.
Следует обратить внимание на следующий момент. Например, если взять достаточно представительную выборку черепов какого-нибудь вида млекопитающего и выяснить распределение по такому параметру, как длина черепа, то мы должны получить нормальное распределение, представленное колоколообразной кривой. Но, если мы возьмем по одному черепу каждого вида млекопитающего и выясним распределение по этому же параметру, то получим ранговое распределение.
Вполне очевидно, что смысл правила Виллиса можно оценить при сравнении этих двух типов распределений (нормальное и ранговое), которые мы будем рассматривать как альтернативные (точнее было бы сказать, что речь идет о сравнении "двухвостых" и "однохвостых" статистик). Но предварительно рассмотрим предлагавшиеся объяснения правила Виллиса.
В правиле Виллиса А.И. Кафанов и В.В. Суханов (1981) не видят биологического смысла и считают, что объем таксона определяется соображениями удобства. В своей работе они приводят обоснования тому, что распределение Ципфа отражает плотность распределения случайной величины. Однако очевидно, что альтернативная гипотеза должна основываться на модели, описывающей распределение неслучайной, зависимой величины. Поэтому точка зрения этих авторов не может быть противопоставлена, например, тому объяснению, которое предложил Э. Майр (1971), так как независимость видообразования и дивергенции признаков постулирует именно случайность появления новых видов (точнее – случайный характер распределения признаков, с помощью которых дифференцируются виды). Так как количество видов характеризует объем рода и, следовательно, данное распределение отражает именно распределение родов по их объему, то при переводе эволюционной терминологии (видообразование, дивергенция) на язык таксономии можно говорить об отсутствии корреляции между объемом родов и признаками, с помощью которых характеризуются роды. Альтернативной гипотезой естественно будет наличие корреляции между объемом и характеристикой родов.
Математическую формулировку правила Виллиса А.Э. Филиппов (1984) выводит, рассматривая его как следствие дискретности процесса видообразования, определяемого в свою очередь случайностью обнаружения свободных экологических ниш. Альтернативная гипотеза, следовательно, должна основываться на непрерывности процесса видообразования, определяемого закономерным обнаружением свободных экологических ниш. Надо сказать, что представление о непрерывности процесса видообразования является преобладающим среди биологов, однако оно никак не связывается с процессом закономерного обнаружения свободных экологических ниш.
Используя модель географического видообразования, В.К. Равин и А.В. Рубанович (1982) также выводят математическую формулировку правила Виллиса, хотя они и признают, что математический вывод формулы независим от предположений относительно конкретного механизма видообразования.
Н.А. Заренков (1988) считает, что соотношение частот родов и видов, описываемое правилом Виллиса, получается вследствие независимости сходства и приспособленности.
На основе модели эволюции, в которой видообразование и вымирание происходят случайно и независимо, а новые роды формируются путем случайного дробления вымирающих родов, также получается ранговое распределение объемов ныне существующих родов (Reed, Hughes, 2002).
Правило Виллиса рассматривается так же, как отражение зависимостей в рамках структур метауровня на природное биологическое разнообразие или как зависимость систематики от содержательных концептуальных моделей, в рамках которых выполняется принцип оптимальности классификаций (Pavlinov et al., 1995), что естественно нисколько не противоречит мнениям, приведенным выше. Альтернативной гипотезой в этом случае будет независимость биологического разнообразия или систематики от концептуальных моделей или структур более высокого уровня.
А.В. Свиридов (1994) предполагает вероятностный характер распределения родовых признаков, дифференцирующих рода друг от друга. Основываясь на анализе определительных ключей, он пришел к мнению, что закон Виллиса связан с законом гомологических рядов Вавилова, так как "… гомологическая изменчивость в стволах пропорциональна расстоянию между ними", что определяется вероятностью "… возникновения одних и тех же изменений признаков в различных стволах в зависимости от расстояния между ними" (Свиридов, 1994, с. 170-171). Эта точка зрения фактически является альтернативой объяснению Э. Майра (1971), так как в конечном счете постулирует связь между объемом родов и дифференциальными признаками.
* * *
Определительные ключи рассматриваются в качестве средства таксономического анализа (Майр, 1971). Учитывая, что А.В. Свиридов (1994) рассматривает правило Виллиса в связи с диагностическими ключами, мне показалось, что анализ характера распределения признаков в них будет представлять значительный интерес.
Основой для анализа послужили ключи, составленные для различных групп организмов и включавшие не менее 50-ти таксонов. Так как в корректно составленном ключе тезы и антитезы должны быть симметричными, т.е. в них должны приводиться одинаковые признаки, но с различными модальностями в тезе и антитезе, то при подсчете учитывались только тезы. В случае, когда в ключе встречались несимметричные тезы и антитезы (например, когда в тезе приводятся 3-4 признака, а в антитезе, как правило, один), и в случае несовпадения признаков в тезе и антитезе учитывались только такие признаки, которые были приведены как в тезе, так и в антитезе. Следует отметить, что отсутствие формализованных названий признаков иногда приводило к затруднениям в их сопоставлении, поэтому мне представляется, что общее количество признаков (табл. 1, 2) оказалось несколько завышенным.
Анализ даже такого небольшого количества ключей дал, на мой взгляд, очень интересные результаты (табл. 1). Следует прокомментировать некоторые статистические параметры, приведенные в этой таблице. Показатель F/T отражает среднее количество дифференциальных признаков, приходящихся на один таксон; его можно рассматривать в определенном смысле как меру морфологического разнообразия таксона (см. ниже). Следует также заметить, что чем меньше показатель F/T, т.е. чем меньше разных признаков задействовано для различения таксонов данной группы, то приходится использовать больше комбинаций признаков для этой цели и, следовательно, следует ожидать более яркого проявления закона гомологических рядов. Показатель S/T отражает среднее количество дифференциальных признаков, с помощью которых проводится различение таксонов. Чем больше величина этого показателя, т.е. чем больше признаков привлечено для различения пары таксонов, то либо таксоны плохо различимы и для повышения точности определения приходится использовать больше признаков, либо, наоборот, таксоны хорошо дифференцированы по большому комплексу признаков.
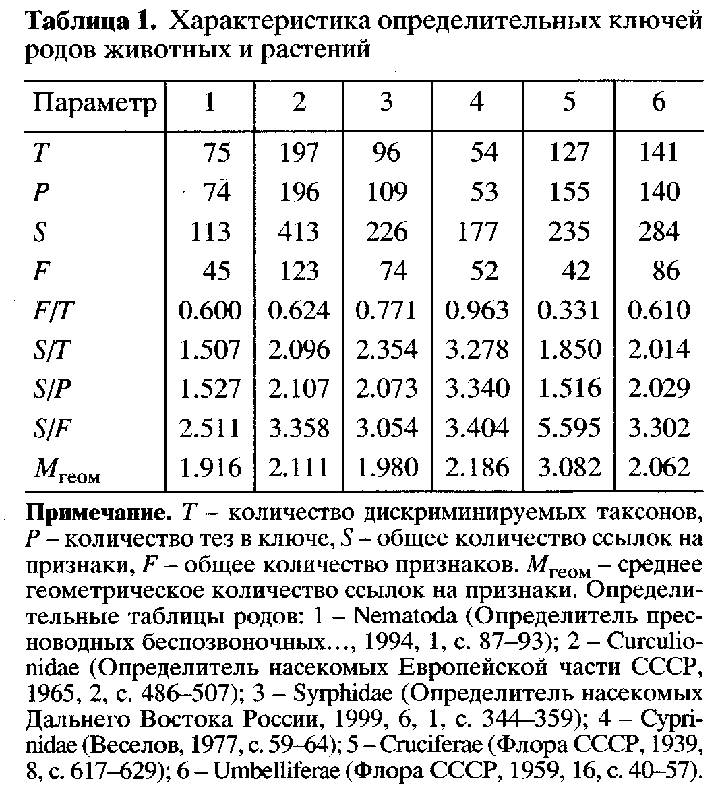
Распределение признаков по количеству ссылок на них является близким к ранговому, или в логарифмических координатах – близким к линейному (рис. 1). Полученный результат в первом приближении можно рассматривать как свидетельство в пользу точки зрения А.В. Свиридова (1994) о связи правила Виллиса с законом гомологических рядов Н.И. Вавилова.
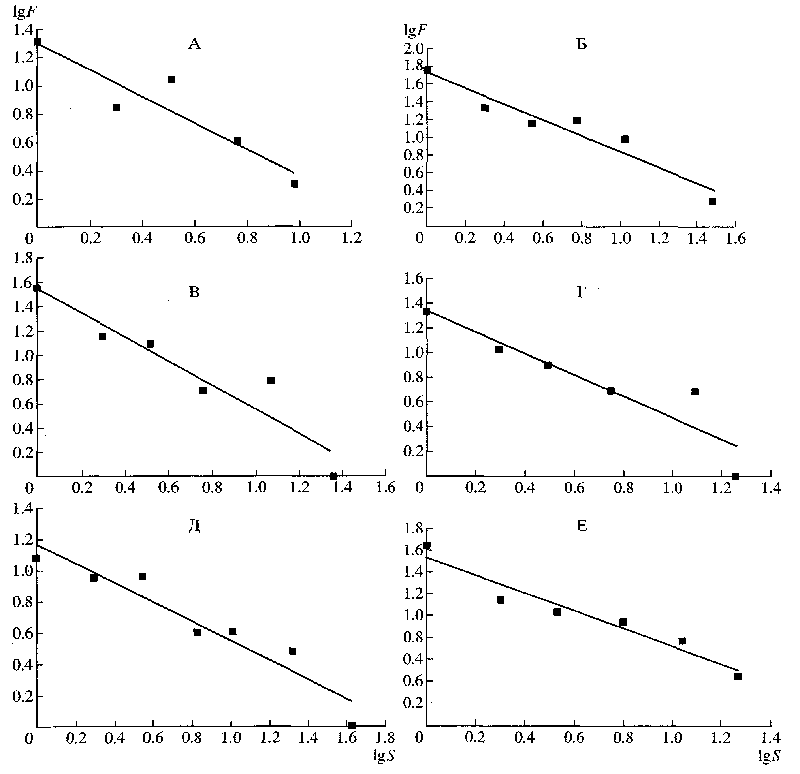
Рис. 1. Распределение признаков по количеству ссылок на них в ключах для определения родов разных групп организмов: lgS - логарифм количества ссылок на признаки; lgF - логарифм количества признаков; А - Nematoda; Б - Curculionidae; В - Syrphidae; Г - Cyprinidae; Д - Cruciferae; E - Umbelliferae.
Распределение семейств по количеству родов также ближе к ранговому (в логарифмических координатах – линейному), чем к нормальному (рис. 2). Интересно, если исходить из степени приближения указанных распределений к линейному, то оказывается, что для наземных позвоночных, исключая амфибий, и растений завышено количество семейств, включающих один род, тогда как у амфибий завышено количество семейств, включающих два рода. Хотя вполне может быть, что сравнительно большое количество семейств с двумя родами у последних отражает таксономические реалии этого класса позвоночных.
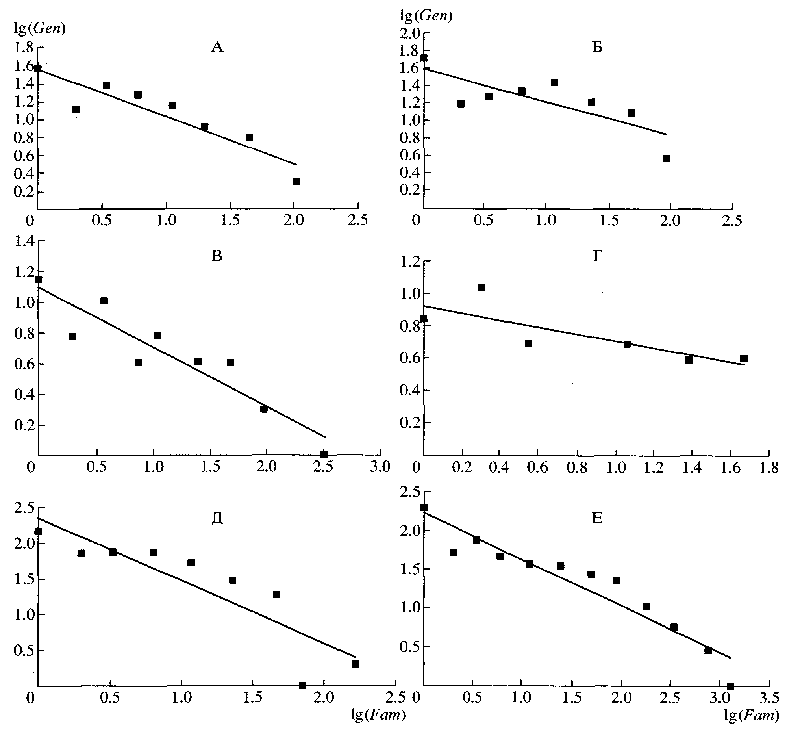
Рис. 2. Распределение семейств по количеству родов: А - млекопитающие (по: Walker, 1968); Б - птицы (по: Беме, Флинт, 1994); В - пресмыкающиеся (по: Ананьева и др., 1988); Г - земноводные (по: Ананьева и др., 1988); Д - рыбы (по: Решетников и др., 1989); Е - покрытосеменные (по: Тахтаджян, 1987).
Анализ ключей для определения семейств (табл. 2) показывает, что в них по сравнению с ключами для определения родов (табл. 1) использовано больше признаков (показатель F/T больше единицы, тогда как в случае ключей для определения родов он меньше). Этот результат также можно трактовать в пользу мнения А.В. Свиридова как свидетельство того факта, что эффект гомологических рядов на уровне семейств проявляется гораздо слабее, чем на уровне родов.

Однако распределение признаков по количеству ссылок на них в ключах для определения семейств также является близким к ранговому, или в логарифмических координатах – близким к линейному (рис. 3). Если бы существовала связь между характером распределения дифференциальных признаков и правилом Виллиса через посредство закона гомологических рядов Вавилова, то в этом случае следовало бы ожидать худших результатов, по сравнению с характером распределения признаков в ключах для определения родов.
Рис. 3. Распределение признаков по количеству ссылок на них в ключах для определения семейств разных отрядов насекомых: lgS - логарифм количества ссылок на признаки; lgF — логарифм количества признаков; А - Coleoptera; Б - Diptera; В - Hymenoptera; Г - Lepidoptera.
Итак, распределение таксонов по их объему и распределение дифференциальных признаков по частоте их использования в ключе являются ранговыми и, видимо, независимыми. Однако вполне возможно, что указанные распределения независимо друг от друга отражают какую-то общую биологическую закономерность (Pavlinov et al., 1995).
С математической точки зрения, то, что распределено по нормальному закону, характеризуется максимальной энтропией или максимальной неупорядоченностью (Чайковский, 2001). Если рассматривать ранговые распределения как альтернативные нормальным, то тогда они характеризуют совокупности, которым в той или иной мере присуща упорядоченность. С этой точки зрения биологическое разнообразие, характеризующееся как раз ранговым распределением по различным параметрам, является упорядоченным или самоорганизованным. Иными словами, биологическое разнообразие представляет собою Естественную систему.
Это утверждение позволяет осветить проблему онтологических оснований биологических классификаций. Очевидно, что получаемые систематиками частные классификации будут осмысленными лишь в том случае, если они основываются на предварительно принятой биологически содержательной теории (Павлинов, 1995, 2001, 2003). Самоорганизованность, упорядоченность биологического разнообразия не позволяют рассматривать Естественную систему как эпифеномен случайных эволюционных процессов.
Однако в литературе в качестве такой возможной причины упорядоченности рассматривается фактически лишь наличие памяти о прошлом состоянии, которое считается характерным в том числе и для ветвящихся процессов (Чайковский, 2001). Эта точка зрения подкрепляется и математическими расчетами. Так, с огласно математическим моделям, ранговые распределения появляются вследствие наложения двух ветвящихся процессов, например, возникновения видов и возникновения родов (Yule, 1924 – цит. по: Чайковский, 2001) или когда видообразование и вы мирание видов случайно и независимо, а возникновение новых родов происходит в результате случайного дробления вымирающих родов (Reed, Hughes, 2002). При этом значение придается наличию положительной обратной связи, когда при одинаковой вероятности появления нового вида, большие роды имеют больше шансов увеличить свой объем по сравнению с небольшими.
Принимая во внимание тот факт, что смена поколений особей также является ветвящимся процессом, выясняется, что таксонообразование оказывается не синхронизированным с указанным процессом. Даже скорее всего здесь проявляется обратная зависимость (Расницын, 1987). По представлениям некоторых биологов, темп таксонообразования не является чисто случайным, а оказывается в зависимости от биоценотических факторов, не учитываемых в модели ветвящегося процесса (Красилов, 1969; Жерихин, 1986).
С этой точки зрения филогенетическую систематику и кладистику следует рассматривать лишь как попытку восстановить ход таксоногенеза, но не попытку выявить Естественную систему. Если учитывать следующие моменты, то вряд ли эти попытки можно признать удачными. Во-первых, отсутствует синхрония между появлением инноваций, по которым восстанавливается таксоногенез, и таксонообразованием (Павлинов, 1990). Во-вторых, филогенетические модели основаны на принятии определенного способа появления инноваций, который может быть далек от реальности (Шишкин, 1984, 1988; Гродницкий, 2001а, б). В-третьих, филогенетические модели на низших таксономических уровнях получаются более противоречивыми, чем на высших, хотя, исходя из принимаемых теоретических оснований, должно быть наоборот. Этот момент очень интересный и его следует обсудить более подробно.
Как было показано выше (ср. табл. 1 и 2), количество дифференциальных признаков на низших таксономических уровнях меньше по сравнению с высшими. В дополнение к указанному материалу можно добавить то, что количество дифференциальных признаков, привлекаемых для различения отрядов, еще выше. Так, в случае млекопитающих показатель F/T равен 2.75 (ключ по: Кузнецов, 1975), 2.88 (ключ по: Бобринский и др., 1965), 2.83 (ключ по: Павлинов и др., 1995), в случае птиц 1.74 (ключ по: Кузнецов, 1974б; 27 отрядов; 47 признаков), 2.44 (ключ по: Иванов, Штегман, 1964; 18 отрядов, 44 признака), в случае рыб 2.4 (ключ по: Кузнецов, 1974а).
На первый взгляд может показаться, что, если отряды больше по объему семейств, а семейства – родов, то и их разнообразие должно быть выше. В целом это утверждение верно, однако выясняются некоторые интересные частности. Например, при сравнении ключей для определения семейств Coleoptera и родов Curculionidae выясняется, что всего использовано 194 признака, из которых общими являются 27 (13.9%), а в случае Diptera и Syrphidae из 232 признаков общими являются только 9 (3.9%). Получается, что дискриминация семейств в отрядах и родов в семействах проводится с использованием разных признаков. Так как в современных эволюционных моделях дарвиновской традиции отсутствуют формальные запреты на изменение (ограничение) разнообразия в процессе эволюции, то при использовании различного набора признаков при дискриминации таксонов различного уровня следовало бы ожидать примерно одинаковой величины показателя F/T на разных таксономических уровнях.
Итак, на основании вышесказанного получается, что трудность построения филогении низших таксонов связана именно с их меньшим разнообразием по сравнению с высшими таксонами, что выражается в недостатке дифференциальных признаков.
Еще один момент. Как уже говорилось выше, показатель F/T можно рассматривать в качестве меры морфологического разнообразия. Значения этого показателя в случае ключей для определения отрядов млекопитающих, выполненных разными исследователями и на разном таксономическом объеме, очень близки и сопоставимы с аналогичными показателями для определения отрядов рыб и птиц (в случае ключа, выполненного А.И. Ивановым и Б.К. Штегманом). С учетом этих данных сопоставление двух ключей для определения отрядов птиц показывает, что они выполнены на одном таксономическом объеме с использованием сходного количества признаков. Различие в величине показателя F/T для этих ключей обусловлено только различным принятым количеством отрядов. На основании вышесказанного можно сделать вывод, что представление Б.А. Кузнецова о количестве отрядов птиц является завышенным по сравнению с точкой зрения А.И. Иванова и Б.К. Штегмана.
В целом даже этих небольших данных вполне достаточно, чтобы сделать вывод в пользу представлений об ограниченности изменчивости и таксономическом ранжировании дифференциальных признаков (Васильева, 1990, 1998; Любарский, 1991).
Хотелось бы подчеркнуть, что ранговые распределения отражают наличие упорядоченности биологической системы в соответствии с величиной какого-либо параметра. Очевидно, что эти параметры (объем таксона или частоты модальностей дифференциальных признаков) не могут являться непосредственной причиной порядка Естественной системы и не позволяют напрямую ее определить. Если рассматривать жизнь как процесс, в ходе которого энтропия уменьшается и, следовательно, увеличивается упорядоченность, то в таком случае приходится признать, что упорядоченность изначально присуща живому. Если это так, то Естественная система, понимаемая как упорядоченная совокупность таксонов, в логическом смысле первична и основные проблемы заключаются не в выяснении причин упорядоченности и процесса ее формирования, а в выявлении структуры таксономического разнообразия.
Итак, "… разнообразие возникает вследствие того, что на ограниченном множестве пере менных, каждая из которых изменяется по общему правилу, но в разных отношениях, может возникать очень большое число комбинаций, в конечном итоге обеспечивающее индивидуальность любого биологического образования при подчинении его некоторой общей схеме самоподобного преобразования" (Пузаченко, Пузаченко, 1996, с. 38). Другими словами, разнообразие формируется в соответствии с собственными законами (Pavlinov et al., 1995), и в этом случае структура разнообразия не зависит от способа формирования, т.е. от ее истории. Учитывая также ситуацию с непроработанностью принципов восстановления филогенеза, а также представлением о невосстановимости филогенеза в единственном точном варианте (см.: Мейен, 1984), очевидно, что структура Естественной системы должна выявляться на основе собственных законов, а не филогенетических реконструкций.
Очень интересна проблема фрактальности Естественной системы. Представления о фракталах подробно разработаны в математике (Федер, 1991; Пайтген, Рихтер, 1993; Мандельброт, 2002). Одним из основных свойств фракталов является самоподобие. Это означает, что выделенная часть фрактала по каким-то характеристикам подобна целому. Соответственно разные части подобны друг другу.
Самоподобием характеризуются статистика вымирания (Sole et al., 1997), структура филогенетических деревьев (Nottale et al., 2000), структура таксономического разнообразия (Пузаченко, Пузаченко, 1996; Chu, Adami, 1999), структура экологических сообществ (Gisiger, 2001; Halley et al., 2004). Анализ структуры разнообразия млекопитающих и птиц показал, что "… получить такое подобие чисто случайно весьма затруднительно, и можно считать, что таксономические классификации с учетом всех проблем, связанных с их построением, все-таки отражают собственные законы формирования разнообразия" (Пузаченко, Пузаченко, 1996, с. 35).
Итак, если рассматривать Естественную систему как фрактал, то ее части подобны целому и друг другу. Это подобие является структурным и выражается в ранговых распределениях таксонов по их объему, а так же, как было показано выше, в ранговых распределениях дифференциальных признаков по частоте их использования. Последнее распределение можно рассматривать как отражающее интенсиональную характеристику таксона.
В отличие от математических фракталов, которые дробимы до бесконечности, реальные фракталы имеют предел делимости. В этом случае низшей частью Естественной системы как фрактала будет такая часть, которая по структуре будет подобна целому, т.е. в ней будет выдерживаться с экстенсиональной стороны ранговое распределение таксонов по объему и с интенсиональной стороны ранговое распределение дифференциальных признаков по частоте их использования. Этой низшей частью не может быть вид, так как его невозможно охарактеризовать с интенсиональной стороны ранговым распределением. Также вид является объектом иной природы по сравнению с таксонами (Поздняков, 2003). Поэтому низшей единицей Естественной системы будет являться таксон родового ранга. Кстати, Э. Майр (1971) также рассматривает роды как самые низшие единицы из всех категорий, устанавливаемые сравнительным методом.
Логически можно предположить наличие двух способов формирования фрактала. Во-первых, путем дробления целого на последовательно уменьшающиеся части. Во-вторых, путем "умножения" единиц с образованием более крупных частей. Скорее всего, оба эти способа существуют в природе, но их описание возможно с помощью разных понятийных аппаратов, причем, видимо, дополнительных друг другу. Исторически признание наличия второго способа формирования Естественной системы связывается с "Происхождением видов" Чарльза Дарвина, причем на основе "умножения" видов с формированием таксонов более высокого ранга. Наличие первого способа формирования Естественной системы – путем дробления таксонов на подтаксоны – фактически провозглашено Вилли Хеннигом в "Основаниях теории филогенетической систематики".
С моей точки зрения, второй процесс – увеличение количества единиц Естественной системы – должен быть связан с образованием новых родов, или таксонообразованием. Первый процесс следует рассматривать с типологической позиции как изменение содержания интенсионала при таксонообразовании.
В связи с вышесказанным возникает проблема реальности Естественной системы и ее частей. Разумеется, Естественная система реальна как целое, как фрактал. Таксон родового ранга реален как универсальная единица Системы. Высшие (надродовые) таксоны являются фрагментами, частями Естественной системы и с определенной точки зрения они тоже реальны, как, например, реальны части лица. Однако с этой же точки зрения они не являются ни целостностями, ни имеют индивидных свойств и потому не обладают сущностью. Однако проблема сущности слишком сложна и ее обсуждение требует отдельной статьи.
Следующим основным свойством фракталов является их дробная размерность, которая превышает их топологическую размерность. Биологические классификации, которые чаще всего представляют как список таксонов, расположенный в определенном порядке, имеют в этом случае топологическую размерность, равную единице. Одномерную топологию имеют классификации и в случае представления их в виде дендрограммы. Двумерную топологию имеют биологические классификации, выраженные в форме таблицы (Соболев, 1914; Догель, 1923; Шимкевич, 1929; Васильева, 1985), которая находит определенные теоретические обоснования (Васильева, 1987, 1990, 1993).
Очевидно, что список таксонов не является адекватным способом выражения Естественной системы, так как он в состоянии точно отразить лишь некую строго линейную последовательность. Так как изображение Системы в виде древа от Э. Геккеля до нынешних дней претерпело существенные изменения, да и современные представления, надо полагать, не являются окончательными, то неясно, насколько точно дендрограммы отражают реальность. В данном случае речь идет не о степени соответствия гипотетических древес реальности, а о принципах построения дендрограмм. Например, фактические данные, а также основанные на них модели говорят о том, что среднее количество подтаксонов в таксоне примерно равно трем (Пузаченко, Пузаченко, 1996). В соответствии с этими данными при построении дендрограмм необходимо использовать трихотомию, тогда как методы кладистики вменяют строгое применение дихотомии. То же самое относится и к двумерным табличным классификациям. Пока неясно, можно ли фактические данные о трехчленности таксонов рассматривать в качестве свидетельства трехмерной топологии Естественной системы? Если это так, то фрактальная размерность Естественной системы заключается в промежутке от трех до четырех.
* * *
В заключение хотелось бы подчеркнуть, что фактические данные свидетельствуют в пользу того, что органическое разнообразие упорядочено в соответствии со своими собственными законами. Естественную систему следует рассматривать как фрактал, обладающий свойствами целого. Части этого фрактала – таксоны – подобны друг другу и целому по структуре, выражающейся в характере распределения таксонов по их объему, а также в характере распределения дифференциальных признаков по частоте их использования, что описывается правилом, или законом Виллиса.
Таксоны родового ранга в этом случае являются единицами Естественной системы, имеющими универсальный характер, т.е. сопоставимыми в пределах любых групп живых существ (см. Майр, 1971). Однако теоретическая разработка концепции рода, аналогичная таковой концепции вида, находится пока в зачаточном состоянии.
Для выявления Естественной системы имеет значительный интерес определение ее топологической размерности, или, скорее, аналога топологической формы. Так как в настоящее время Естественная система может быть изображена различными способами (списком таксонов, дендрограммой, таблицей), имеющими определенную научно-историческую традицию и определенные теоретические мотивировки, то здесь еще требуется выработка общего подхода, хотя вполне возможно, что размерность Естественной системы не является постоянной и может быть различной для разных ее частей.
Автор очень признателен Д.А. Милько, А.В. Баркалову, В.К. Зинченко за помощь при подборе определительных ключей, а Д.А. Милько – за полезное обсуждение некоторых терминов.
СПИСОК ЛИТЕРАТУРЫ
Ананьева Н.Б., Боркин Л.Я., Даревский И.С., Орлов Н.Л., 1988. Пятиязычный словарь названий животных. Амфибии и рептилии. М.: Рус. яз. 560 с.
Беме Р.Л., Флинт В.Е., 1994. Пятиязычный словарь названий животных. Птицы. М.: Рус. яз., РУССО. 845 с.
Бобринский Н.А., Кузнецов Б.А., Кузякин А.П., 1965. Определитель млекопитающих СССР. М.: Просвещение. 382 с.
Васильева Л.Н., 1985. Комбинативный принцип в систематике пиреномицетов // Комаровские чтения. Владивосток: ДВНЦ АН СССР. Вып. 32. С. 14-56.
Васильева Л.Н., 1987. Пиреномицеты и локулоаскомицеты севера Дальнего Востока. Л.: Наука. 257 с.
Васильева Л.Н., 1990. Философия систематики // Философские исследования эволюции живой природы и человека. Владивосток: Изд-во ДВУ. С. 127-161.
Васильева Л.Н., 1993. Платон и систематика // Вести. ДВО РАН. Т. 47. Вып. 1. С. 63-73.
Васильева Л.Н., 1998. Иерархическая модель эволюции // Журн. общ. биологии. Т. 59. № 1. С. 5-23.
Веселов Е.А., 1977. Определитель пресноводных рыб фауны СССР. М.: Просвещение. 238 с.
Голиков А.Н., 1976. О количественных закономерностях процесса дивергенции // Гидробиологические исследования самоочищения водоемов. Л.: Зоол. ин-т АН СССР. С. 90-96.
Гродницкий Д.Л., 2001а. Эпигенетическая теория эволюции как возможная основа нового эволюционного синтеза // Журн. общ. биологии. Т. 62. № 2. С. 99-109.
Гродницкий Д.Л., 20016. Две теории биологической эволюции. Саратов: Научная книга. 160 с.
Догель В., 1923. Ход развития видов в семействе Ophryoscolecidae // Архив русск. протистолог. об-ва. Т. 2. М.; П., С. 89-104.
Жерихин В.В., 1986. Биоценотическая регуляция эволюции // Палеонтол. журн. № 1. С. 3-12.
Заренков Н.А., 1988. Теоретическая биология (Введение). М.: Изд-во МГУ. 216 с.
Иванов А.И., Штегман Б.К., 1964. Краткий определитель птиц СССР. М.; Л.: Наука. 528 с.
Кафанов А.И., Суханов В.В., 1981. О зависимости между числом и объемом таксонов // Журн. общ. биологии. Т. 42. № 3. С. 345-350.
Корона В.В., 1987. Основы структурного анализа в морфологии растений. Свердловск: Изд-во Урал, ун-та. 272 с.
Красилов В.А., 1969. Филогения и систематика // Проблемы филогении и систематики. Владивосток: БПФ ДВО. С. 12-30.
Кузнецов Б.А., 1974а. Определитель позвоночных животных фауны СССР. М.: Просвещение. Ч. 1.190 с.
Кузнецов Б.А., 19746. Определитель позвоночных животных фауны СССР. М.: Просвещение. Ч. 2. 226 с.
Кузнецов Б.А., 1975. Определитель позвоночных животных фауны СССР. М.: Просвещение. Ч. 3. 208 с.
Любарский Г.Ю., 1991. Объективация категории таксономического ранга // Журн. общ. биологии. Т. 52. №5. С. 613-626.
Майр Э., 1971. Принципы зоологической систематики. М.: Мир. 454 с.
Манделъброт Б., 2002. Фрактальная геометрия природы. М.: Ин-т компьютер, исслед. 655 с.
Мейен С.В., 1984. Принципы исторических реконструкций в биологии // Системность и эволюция. М.: Наука. С. 7-32.
Определитель насекомых Европейской части СССР, 1965. Т. 2. М.; Л.: Наука. 668 с.
Определитель насекомых Европейской части СССР, 1969. Т. 5. Ч. 1. М.; Л.: Наука. 809 с.
Определитель пресноводных беспозвоночных России и сопредельных территорий, 1994. Т. 1. Низшие беспозвоночные. СПб.: Зоол. ин-т РАН. 395 с.
Определитель насекомых Дальнего Востока России, 1995. Т. 4. Сетчатокрылые, скорпионницы, перепончатокрылые. Ч. 1. СПб.: Наука. 606 с.
Определитель насекомых Дальнего Востока России, 1997. Т. 5. Ручейники и чешуекрылые. Ч. 1. Владивосток: Дальнаука. 540 с.
Определитель насекомых Дальнего Востока России, 1999. Т. 6. Двукрылые и блохи. Ч. 1. Владивосток: Дальнаука. 665 с.
Павлинов И.Я., 1990. Кладистический анализ (методологические проблемы). М.: Изд-во МГУ. 160 с.
Павлинов И.Я., 1995. Классификация как гипотеза: вхождение в проблему // Журн. общ. биологии. Т. 56. №4. С. 411-424.
Павлинов И.Я., 2001. Концепции систематики и концепции биоразнообразия: проблема взаимодействия // Журн. общ. биологии. Т. 62. № 4. С. 362-366.
Павлинов И.Я., 2003. В защиту "зависимой" систематики // Териологические исследования. Вып. 3. СПб.: Зоологический институт РАН. С. 41-59.
Павлинов И.Я., Борисенко А.В., Крускоп СВ., Яхонтов Е.Л., 1995. Млекопитающие Евразии. Т. 2. Non-Rodentia. M.: Изд-во МГУ. 336 с.
Пайтген Х.-О., Рихтер П.Х., 1993. Красота фракталов: Образы комплексных динамических систем. М.: Мир. 176 с.
Поздняков А.А., 2003. Проблема индивидности в таксономии // Журн. общ. биологии. Т. 64. № 1. С. 55-64.
Пузаченко Ю.Г., Пузаченко А.Ю., 1996. Семантические аспекты биоразнообразия // Журн. общ. биологии. Т. 57. № 1. С. 5-43.
Равин В.К., Рубанович А.В., 1982. Географическое видообразование и количественная структура таксона // ДАН. Т. 263. № 1. С. 247-250.
Расницын А.П., 1987. Темпы эволюции и эволюционная теория (гипотеза адаптивного компромисса) // Эволюция и биоценотические кризисы. М.: Наука. С. 46-64.
Решетников Ю.С., Котляр А.Н., Расс Т.С, Шатуновский М.И., 1989. Пятиязычный словарь названий животных. Рыбы. М.: Рус. яз. 734 с.
Свиридов А.В., 1994. Ключи в биологической систематике: теория и практика. М.: Изд-во МГУ. 224 с.
Соболев Д., 1914. Наброски по филогении гониатитов // Изв. Варшавского политехн. ин-та. Вып. 1. С. 1-191.
Тахтаджян А.Л., 1987. Система магнолиофитов. Л.: Наука. 439 с.
Федер Е., 1991. Фракталы. М.: Мир. 260 с.
Филиппов А.Э., 1984. Дискретное видообразование и закон Виллиса // Журн. общ. биологии. Т. 45. № 3. С. 410-418.
Флора СССР, 1939. Т. 8. М.; Л.: АН СССР. 695 с.
Флора СССР, 1950. Т. 16. М.; Л.: АН СССР. 648 с.
Чайковский Ю.В., 2001. О природе случайности. М.: Центр системных исследований. 272 с.
Шимкевич В.М., 1929. Многоколенчатые (Pantopoda). Вып. 1. Л.: Зоологический институт АН СССР. 224 с.
Шишкин М.А., 1984. Фенотипические реакции и эволюционный процесс (еще раз об эволюционной роли модификаций) // Экология и эволюционная теория. Л.: Наука. С. 196-216.
Шишкин М.А., 1988. Эволюция как эпигенетический процесс // Современная палеонтология. Т. 2. М.: Недра. С. 142-169.
Apic G., Gough J., Teichmann S.A., 2001. Domain combinations in archaeal, eubacterial and eukaryotic proteomes // J. Mol. Biol. V. 310. P. 311-325.
Chu J., Adami Ch., 1999. A simple explanation for taxon abundance patterns // PNAS. V. 96. P. 15017-15019.
Gisiger Т., 2001. Scale invariance in biology: coincidence or footprint of a universal mechanism? // Biol. Rev. V. 76. P. 161-209.
Halley J.M., Hartley S., Kallimanis A.S., Kunin W.E., Lennon J.J., Sgardelis S.P., 2004. Uses and abuses of fractal methodology in ecology // Ecology Letters. V. 7. P. 254-271.
Kuznetsov V.A., 2003. Family of skewed distributions associated with the gene expression and proteome evolution // Signal Processing. V. 83. P. 889-910.
Nottale L., Outline J., Grou P., 2000. On the fractal structure of evolutionary trees // Fractals in Biology and Medicine. V. 3. P. 247-258.
Pavlinov I.Ja., Puzachenko Yu.G., Puzachenko A.Yu., Lubarsky G.Yu., 1995. To Zipf or not to Zipf, or why are there so few scientists supposing there are no genera in the nature at all? // Zhurnal obshchei biologii (J. general biology). V. 56. № 1. P. 152-158.
Reed W.J., Hughes B.D., 2002. On the size distribution of live genera // J. Theor. Biol. V. 217. P. 125-135.
Sole R.V., Manrubia S.C., Benton M., Bak P., 1997. Self-similarity of extinction statistics in the fossil record // Nature. V. 388. P. 764-767.
Walker E.P., 1968. Mammals of the world. Baltimore: John Hopkins Pr. V. 1. XLVIII + 644 p.